Chapter 3 Playing With Numbers (Concepts)

Factors and Multiples

In this chapter, we will explore the fascinating world of numbers by looking at how they are built (using factors) and how they grow (using multiples). We will also learn about different types of numbers and discover some easy tricks (divisibility tests) to know if a number can be exactly divided by another.

---

Factors

When one number divides another number completely, leaving no remainder, the divisor is called a factor of the number being divided (the dividend). Think of factors as the numbers you can multiply together to get a specific number.

For example, let's consider the number $12$. We want to find the numbers that divide $12$ exactly.

• $12 \div 1 = 12$ (remainder 0)
• $12 \div 2 = 6$ (remainder 0)
• $12 \div 3 = 4$ (remainder 0)
• $12 \div 4 = 3$ (remainder 0)
• $12 \div 5 = 2$ (remainder 2) - $5$ is NOT a factor of $12$.
• $12 \div 6 = 2$ (remainder 0)
• $12 \div 12 = 1$ (remainder 0)

The numbers that divide $12$ exactly are $1, 2, 3, 4, 6,$ and $12$. So, these are the factors of $12$.

Alternatively, we can find factors by thinking about multiplication pairs that give the number. To find the factors of $18$, we look for pairs of whole numbers whose product is $18$:

$1 \times 18 = 18$

$2 \times 9 = 18$

$3 \times 6 = 18$

If we continue, we get $6 \times 3$, $9 \times 2$, $18 \times 1$, which are just the same pairs in reverse order. The numbers involved in these multiplication pairs ($1, 18, 2, 9, 3, 6$) are the factors.

So, the factors of $18$ are $1, 2, 3, 6, 9,$ and $18$.

---

Properties of Factors

Here are some important things to remember about factors:

• The number $1$ is a factor of every number. This is because any number divided by $1$ gives the number itself as the quotient with a remainder of $0$.
• Every number is a factor of itself. This is because any number divided by itself gives $1$ as the quotient with a remainder of $0$.
• Every factor of a number is an exact divisor of that number (leaving no remainder). This is the definition of a factor.
• Every factor of a given number is less than or equal to the number. For example, the factors of $12$ are $1, 2, 3, 4, 6, 12$. None of them are greater than $12$.
• The number of factors of a given number is finite. You can always list all the factors of any number because they must be less than or equal to the number itself.

---

Multiples

A multiple of a number is the result of multiplying that number by any natural number ($1, 2, 3, ...$). Think of multiples as the numbers you get when you say the multiplication table of a number.

For example, to find the multiples of $5$, we multiply $5$ by $1, 2, 3, 4,$ and so on:

$5 \times 1 = 5$

$5 \times 2 = 10$

$5 \times 3 = 15$

$5 \times 4 = 20$

$5 \times 5 = 25$

and we can continue this process indefinitely.

So, the multiples of $5$ are $5, 10, 15, 20, 25, 30, 35, ...$

---

Properties of Multiples

Here are some important things to remember about multiples:

• Every number is a multiple of itself. (Since Number $\times 1 =$ Number).
• Every multiple of a number (except zero) is greater than or equal to that number. For example, the multiples of $5$ are $5, 10, 15, 20, ...$. They are all $5$ or larger. (Note: While $0$ is a multiple of every number, we usually refer to multiples formed by multiplying by natural numbers $1, 2, 3, ...$).
• The number of multiples of a given number is infinite. Since there are infinitely many natural numbers ($1, 2, 3, ...$), you can keep multiplying the number by larger and larger natural numbers to get more multiples.

---

Relationship between Factors and Multiples

Factors and multiples are two sides of the same coin. Their relationship is inverse.

If 'a' is a factor of 'b', then 'b' is a multiple of 'a'.

• $3$ is a factor of $12 \iff 12$ is a multiple of $3$.
• $6$ is a factor of $18 \iff 18$ is a multiple of $6$.

---

Common Factors and Common Multiples

Common Factors

Common factors are factors that are shared by two or more numbers.

To find the common factors of two numbers, we list the factors of each and then find the ones that appear in both lists.

Example: Find the common factors of 12 and 18.

• Factors of 12 are: 1, 2, 3, 4, 6, 12.
• Factors of 18 are: 1, 2, 3, 6, 9, 18.

The numbers that are in both lists are 1, 2, 3, and 6. So, the common factors of 12 and 18 are 1, 2, 3, 6.

The largest of these common factors is 6. This is called the Highest Common Factor (HCF) or Greatest Common Divisor (GCD).

Common Multiples

Common multiples are multiples that are shared by two or more numbers.

To find common multiples, we list the multiples of each number and find the ones that appear in both lists.

Example: Find the common multiples of 4 and 6.

• Multiples of 4 are: 4, 8, 12, 16, 20, 24, 28, 32, 36, ...
• Multiples of 6 are: 6, 12, 18, 24, 30, 36, ...

The numbers that are in both lists are 12, 24, 36, and so on. The common multiples are 12, 24, 36, ... (this list is infinite).

The smallest of these common multiples is 12. This is called the Lowest Common Multiple (LCM).

---

Answer:

---

Answer:

Types of Natural Numbers

Natural numbers, starting from $1$ ($1, 2, 3, 4, 5, ...$), can be grouped or classified into different types based on their properties. One of the main ways to classify natural numbers is based on their factors.

---

Even and Odd Numbers

Natural numbers can be divided into two groups: those that are exactly divisible by $2$, and those that are not.

Even Numbers: Numbers that are exactly divisible by $2$ (leaving a remainder of $0$) are called even numbers. You can always pair up a collection of objects if their total number is even.

A quick way to identify an even number is to look at its last digit (the digit in the Ones place). Even numbers always end in $0, 2, 4, 6,$ or $8$.

Examples: $2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, ..., 54, ..., 100, ...$

Odd Numbers: Numbers that are not exactly divisible by $2$ are called odd numbers. When you divide an odd number by $2$, there is always a remainder of $1$. You cannot perfectly pair up a collection of objects if their total number is odd.

Odd numbers always end in $1, 3, 5, 7,$ or $9$.

Examples: $1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, ..., 53, ..., 101, ...$

---

Prime and Composite Numbers

Natural numbers greater than $1$ can be classified based on the number of factors they have.

Prime Numbers: A prime number is a natural number greater than $1$ that has exactly two distinct factors: the number $1$ and the number itself.

Let's find the factors for some small natural numbers greater than $1$:

• Factors of $2$: $1$ and $2$. (Exactly two factors) $\implies$ $2$ is a prime number.
• Factors of $3$: $1$ and $3$. (Exactly two factors) $\implies$ $3$ is a prime number.
• Factors of $4$: $1, 2,$ and $4$. (Three factors) $\implies$ $4$ is not a prime number.
• Factors of $5$: $1$ and $5$. (Exactly two factors) $\implies$ $5$ is a prime number.
• Factors of $6$: $1, 2, 3,$ and $6$. (Four factors) $\implies$ $6$ is not a prime number.

Examples of prime numbers: $2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ...$

Important Points about Prime Numbers:

• The smallest prime number is $\mathbf{2}$.
• $\mathbf{2}$ is the only even number that is prime. All other even numbers greater than $2$ have $2$ as a factor in addition to $1$ and themselves, so they have more than two factors.

Composite Numbers: A composite number is a natural number greater than $1$ that has more than two factors.

These are numbers that are not prime (and are greater than $1$). They can be formed by multiplying two smaller natural numbers (greater than $1$).

Examples of composite numbers: $4, 6, 8, 9, 10, 12, 14, 15, \ $$ 16, 18, 20, \ $$ 21, 22, 24, \ $$ 25, 26, 27, \ $$ 28, ...$

Important Point about Composite Numbers:

• The smallest composite number is $\mathbf{4}$.

---

What about the number 1?

The natural number $1$ is unique. Let's look at its factors:

• Factors of $1$: The only number that divides $1$ exactly is $1$ itself. So, $1$ has only one factor.

Based on the definitions of prime and composite numbers:

• A prime number must have exactly two factors. $1$ has only one factor.
• A composite number must have more than two factors. $1$ has only one factor.

Since $1$ does not fit the definition of either a prime number or a composite number, the number $1$ is neither a prime number nor a composite number. It is considered a special number.

---

Sieve of Eratosthenes: Finding Prime Numbers

The Sieve of Eratosthenes is an ancient and simple method for finding all prime numbers up to a specified integer. It works by progressively marking as composite the multiples of each prime.

Steps to find primes up to 100:

1. List all numbers from 1 to 100. Cross out 1 as it is not prime.
2. Circle the first uncrossed number, 2, which is the first prime. Then, cross out all multiples of 2 (4, 6, 8, ...).
3. Move to the next uncrossed number, 3. Circle it as the next prime. Then, cross out all multiples of 3 (6, 9, 12, ...).
4. The next uncrossed number is 5. Circle it and cross out all its multiples (10, 15, 20, ...).
5. The next uncrossed number is 7. Circle it and cross out all its multiples (14, 21, 28, ...).
6. Continue this process. The next prime is 11, but its square (121) is greater than 100, so we can stop.

All the circled or uncrossed numbers left in the grid are the prime numbers up to 100.

The prime numbers between 1 and 100 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

---

Other Types of Numbers

Here are a few other interesting types of number pairs or numbers:

Twin Primes:

Two prime numbers are called twin primes if they have a difference of $2$.

Examples of twin prime pairs:

• $(3, 5)$ because $5 - 3 = 2$, and both $3$ and $5$ are prime.
• $(5, 7)$ because $7 - 5 = 2$, and both $5$ and $7$ are prime.
• $(11, 13)$ because $13 - 11 = 2$, and both $11$ and $13$ are prime.
• $(17, 19)$ because $19 - 17 = 2$, and both $17$ and $19$ are prime.

Co-prime Numbers (or Relatively Prime Numbers):

Two natural numbers are called co-prime numbers (or relatively prime numbers) if they have only one common factor, which is $1$. Their Highest Common Factor (HCF) is $1$.

Let's check some pairs:

• Consider the pair $(4, 9)$:
  Factors of $4$: $1, 2, 4$.
  Factors of $9$: $1, 3, 9$.
  The only common factor is $1$. So, $4$ and $9$ are co-prime numbers.
• Consider the pair $(8, 15)$:
  Factors of $8$: $1, 2, 4, 8$.
  Factors of $15$: $1, 3, 5, 15$.
  The only common factor is $1$. So, $8$ and $15$ are co-prime numbers.
• Consider the pair $(6, 8)$:
  Factors of $6$: $1, 2, 3, 6$.
  Factors of $8$: $1, 2, 4, 8$.
  The common factors are $1$ and $2$. Since they have a common factor other than $1$ (which is $2$), $6$ and $8$ are not co-prime numbers.

Note: Co-prime numbers themselves do not need to be prime numbers. For example, $4$ is composite, $9$ is composite, but the pair $(4, 9)$ is co-prime.

Perfect Numbers:

A perfect number is a natural number for which the sum of all its factors, excluding the number itself, is equal to the number itself. The factors excluding the number itself are also called proper divisors.

Let's check some numbers:

• Consider the number $6$. The factors of $6$ are $1, 2, 3,$ and $6$. The factors excluding $6$ (proper divisors) are $1, 2,$ and $3$.
  Sum of proper divisors $= 1 + 2 + 3 = 6$.
  Since the sum of its proper divisors is equal to the number $6$, $6$ is a perfect number.
• Consider the number $28$. The factors of $28$ are $1, 2, 4, 7, 14,$ and $28$. The proper divisors are $1, 2, 4, 7,$ and $14$.
  Sum of proper divisors $= 1 + 2 + 4 + 7 + 14 = 28$.
  Since the sum of its proper divisors is equal to the number $28$, $28$ is a perfect number.

The next perfect number after $28$ is $496$. Perfect numbers are quite rare.

Divisibility Tests of Natural Numbers

In the previous section, we learned about factors. Finding factors by performing division can be time-consuming, especially for large numbers. Divisibility tests are simple rules or quick checks that help us determine if a number is completely divisible by another number without actually doing the long division. These tests are very useful for finding factors and understanding number properties.

---

Divisibility by 2

A number is divisible by $2$ if its last digit (the digit in the Ones place) is an even digit. The even digits are $0, 2, 4, 6,$ and $8$.

Example: The number $248$ ends in $8$. Since $8$ is an even digit, $248$ is divisible by $2$. ($248 \div 2 = 124$).

Example: The number $357$ ends in $7$. Since $7$ is an odd digit, $357$ is not divisible by $2$. ($357 \div 2 = 178$ with remainder $1$).

Any number that is divisible by $2$ is an even number.

---

Divisibility by 3

A number is divisible by $3$ if the sum of all its digits is divisible by $3$.

Example: Check if $564$ is divisible by $3$.

Sum of the digits of $564 = 5 + 6 + 4 = 15$.

Now, check if $15$ is divisible by $3$. Yes, $15 \div 3 = 5$.

Since the sum of the digits ($15$) is divisible by $3$, the number $564$ is divisible by $3$. ($564 \div 3 = 188$).

Example: Check if $125$ is divisible by $3$.

Sum of the digits of $125 = 1 + 2 + 5 = 8$.

Now, check if $8$ is divisible by $3$. No, $8 \div 3$ leaves a remainder.

Since the sum of the digits ($8$) is not divisible by $3$, the number $125$ is not divisible by $3$.

---

Divisibility by 4

A number is divisible by $4$ if the number formed by its last two digits (the digits in the Tens and Ones places) is divisible by $4$. If the number has only one digit, check if that digit is divisible by $4$. If the number ends with two zeros ($00$), it is also divisible by $4$.

Example: Check if $1416$ is divisible by $4$. The number formed by the last two digits is $16$. Is $16$ divisible by $4$? Yes, $16 \div 4 = 4$.

Since the number formed by the last two digits ($16$) is divisible by $4$, the number $1416$ is divisible by $4$. ($1416 \div 4 = 354$).

Example: Check if $3723$ is divisible by $4$. The number formed by the last two digits is $23$. Is $23$ divisible by $4$? No, $23 \div 4 = 5$ with remainder $3$.

Since the number formed by the last two digits ($23$) is not divisible by $4$, the number $3723$ is not divisible by $4$.

Example: The number $500$ ends in $00$. Therefore, $500$ is divisible by $4$. ($500 \div 4 = 125$).

---

Divisibility by 5

A number is divisible by $5$ if its last digit (the digit in the Ones place) is either $0$ or $5$.

Example: The number $760$ ends in $0$. Therefore, $760$ is divisible by $5$. ($760 \div 5 = 152$).

Example: The number $985$ ends in $5$. Therefore, $985$ is divisible by $5$. ($985 \div 5 = 197$).

Example: The number $432$ ends in $2$. Since the last digit is neither $0$ nor $5$, $432$ is not divisible by $5$.

---

Divisibility by 6

A number is divisible by $6$ if it is divisible by both $2$ and $3$. Remember, $6 = 2 \times 3$, and $2$ and $3$ are co-prime.

Example: Check if $852$ is divisible by $6$.

• Check for divisibility by $2$: The last digit of $852$ is $2$, which is an even digit. So, $852$ is divisible by $2$.
• Check for divisibility by $3$: Sum of the digits of $852 = 8 + 5 + 2 = 15$. $15$ is divisible by $3$. So, $852$ is divisible by $3$.

Since $852$ is divisible by both $2$ and $3$, it is divisible by $6$. ($852 \div 6 = 142$).

Example: Check if $141$ is divisible by $6$.

• Check for divisibility by $2$: The last digit of $141$ is $1$, which is an odd digit. So, $141$ is not divisible by $2$.

Since $141$ is not divisible by $2$, it cannot be divisible by $6$, even though it is divisible by $3$ (Sum of digits $1+4+1=6$, which is divisible by $3$).

---

Divisibility by 8

A number is divisible by $8$ if the number formed by its last three digits (the digits in the Hundreds, Tens, and Ones places) is divisible by $8$. If the number has fewer than three digits, check if the number itself is divisible by $8$. If the number ends with three zeros ($000$), it is also divisible by $8$.

Example: Check if $7816$ is divisible by $8$. The number formed by the last three digits is $816$. Let's check if $816$ is divisible by $8$: $816 \div 8 = 102$. Yes, it is.

Since the number formed by the last three digits ($816$) is divisible by $8$, the number $7816$ is divisible by $8$. ($7816 \div 8 = 977$).

Example: Check if $5324$ is divisible by $8$. The number formed by the last three digits is $324$. Let's check if $324$ is divisible by $8$. $324 \div 8 = 40$ with remainder $4$. No, it is not.

Since the number formed by the last three digits ($324$) is not divisible by $8$, the number $5324$ is not divisible by $8$.

Example: The number $9000$ ends in $000$. Therefore, $9000$ is divisible by $8$. ($9000 \div 8 = 1125$).

---

Divisibility by 9

A number is divisible by $9$ if the sum of all its digits is divisible by $9$. This test is very similar to the divisibility test for $3$.

Example: Check if $459$ is divisible by $9$.

Sum of the digits of $459 = 4 + 5 + 9 = 18$.

Now, check if $18$ is divisible by $9$. Yes, $18 \div 9 = 2$.

Since the sum of the digits ($18$) is divisible by $9$, the number $459$ is divisible by $9$. ($459 \div 9 = 51$).

Example: Check if $1234$ is divisible by $9$.

Sum of the digits of $1234 = 1 + 2 + 3 + 4 = 10$.

Now, check if $10$ is divisible by $9$. No, $10 \div 9 = 1$ with remainder $1$.

Since the sum of the digits ($10$) is not divisible by $9$, the number $1234$ is not divisible by $9$.

Note: If a number is divisible by $9$, it is automatically divisible by $3$. But if a number is divisible by $3$, it is not necessarily divisible by $9$ (e.g., $6$ is divisible by $3$ but not by $9$).

---

Divisibility by 10

A number is divisible by $10$ if its last digit (the digit in the Ones place) is $0$.

Example: The number $670$ ends in $0$. Therefore, $670$ is divisible by $10$. ($670 \div 10 = 67$).

Example: The number $123$ ends in $3$. Since the last digit is not $0$, $123$ is not divisible by $10$.

---

Divisibility by 11

This test is a bit more involved. A number is divisible by $11$ if the difference between the sum of the digits at odd places (starting from the rightmost digit as the 1st place) and the sum of the digits at even places (from the right) is either $0$ or a multiple of $11$ (like $11, 22, 33,$ etc.).

Example: Check if $1331$ is divisible by $11$.

• Identify digits and their places from the RIGHT:
  $1$ (1st place - odd)
  $3$ (2nd place - even)
  $3$ (3rd place - odd)
  $1$ (4th place - even)
• Sum of digits at odd places ($1^\text{st}$ and $3^\text{rd}$) $= 1 + 3 = 4$.
• Sum of digits at even places ($2^\text{nd}$ and $4^\text{th}$) $= 3 + 1 = 4$.
• Difference between the sums $= 4 - 4 = 0$.

Since the difference is $0$, the number $1331$ is divisible by $11$. ($1331 \div 11 = 121$).

Example: Check if $61809$ is divisible by $11$.

• Identify digits and their places from the RIGHT:
  $9$ (1st place - odd)
  $0$ (2nd place - even)
  $8$ (3rd place - odd)
  $1$ (4th place - even)
  $6$ (5th place - odd)
• Sum of digits at odd places ($1^\text{st}$, $3^\text{rd}$, $5^\text{th}$) $= 9 + 8 + 6 = 23$.
• Sum of digits at even places ($2^\text{nd}$, $4^\text{th}$) $= 0 + 1 = 1$.
• Difference between the sums $= 23 - 1 = 22$.

Since the difference is $22$, which is a multiple of $11$ ($22 = 2 \times 11$), the number $61809$ is divisible by $11$. ($61809 \div 11 = 5619$).

Example: Check if $543$ is divisible by $11$.

• Identify digits and their places from the RIGHT:
  $3$ (1st place - odd)
  $4$ (2nd place - even)
  $5$ (3rd place - odd)
• Sum of digits at odd places ($1^\text{st}$, $3^\text{rd}$) $= 3 + 5 = 8$.
• Sum of digits at even places ($2^\text{nd}$) $= 4$.
• Difference between the sums $= 8 - 4 = 4$.

Since the difference is $4$, which is neither $0$ nor a multiple of $11$, the number $543$ is not divisible by $11$.

---

Summary Table of Divisibility Tests

Divisible By	Test
$2$	The last digit is $0, 2, 4, 6,$ or $8$.
$3$	The sum of the digits is divisible by $3$.
$4$	The number formed by the last two digits is divisible by $4$, or the last two digits are $00$.
$5$	The last digit is $0$ or $5$.
$6$	The number is divisible by both $2$ and $3$.
$8$	The number formed by the last three digits is divisible by $8$, or the last three digits are $000$.
$9$	The sum of the digits is divisible by $9$.
$10$	The last digit is $0$.
$11$	The difference between the sum of the digits at odd places (from the right) and the sum of the digits at even places (from the right) is $0$ or a multiple of $11$.

Deciding Whether a Given Number is Prime or Not

A prime number is a natural number greater than $1$ that has only two factors: $1$ and itself. To check if a number is prime, our goal is to find out if it has any other factors. If we can find even one other factor, the number is not prime; it's a composite number.

---

The Primality Test: An Efficient Method

To determine if a number, let's call it '$n$', is prime, we don't need to test every number up to '$n$'. We can use a much more efficient method.

1. Start with the smallest prime number, 2. Check if '$n$' is divisible by 2. If it is (and '$n$' is not 2 itself), then '$n$' is composite, and we can stop.
2. Continue with the next primes. If '$n$' is not divisible by 2, check for divisibility by the next prime numbers in order: 3, 5, 7, 11, and so on.
3. Know when to stop. You don't need to check indefinitely. The key is to stop checking once the prime number you are testing is greater than the square root of '$n$' ($\sqrt{n}$).

Conclusion:

• If '$n$' is divisible by any of these primes, it is a composite number.
• If '$n$' is not divisible by any prime number up to its square root, it is a prime number.

Why do we only need to check up to the square root?

This is a powerful shortcut. Factors always come in pairs. For example, the factors of 36 are paired up: $1 \times 36$, $2 \times 18$, $3 \times 12$, $4 \times 9$, and $6 \times 6$.

Notice that the square root of 36 is 6. In each pair (like $4 \times 9$), one factor is less than or equal to the square root (4 is less than 6), and the other is greater than or equal to the square root (9 is greater than 6).

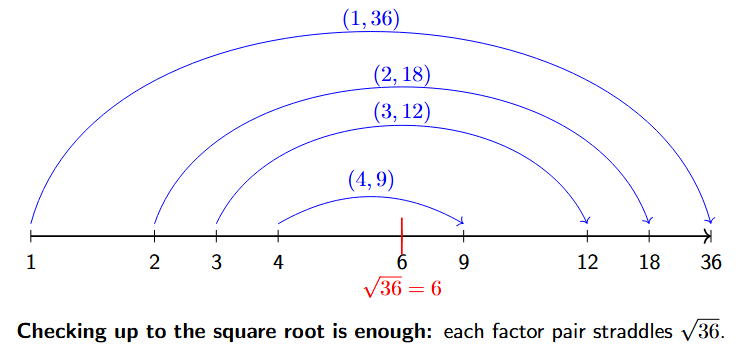
This means if a number '$n$' has a factor larger than its square root, it must also have a smaller factor that is less than its square root. So, by checking for factors only up to the square root, we are guaranteed to find at least one factor from every pair if the number is composite. If we find no factors by the time we reach the square root, we can be certain that no other factors exist.

---

Answer:

---

Answer:

General Properties of Divisibility

Understanding divisibility helps us work with numbers more effectively. There are some general rules or properties about divisibility that apply to natural numbers. Knowing these properties can make solving problems involving factors and multiples easier.

---

Property 1: Divisibility by Factors

If a number is completely divisible by another number, then it is also completely divisible by each and every factor of that divisor number.

Let's take an example: The number $30$ is divisible by $6$ ($30 \div 6 = 5$). The factors of $6$ are $1, 2, 3,$ and $6$.

According to this property, $30$ should be divisible by each of these factors ($1, 2, 3,$ and $6$). Let's check:

• Is $30$ divisible by $1$? Yes, $30 \div 1 = 30$.
• Is $30$ divisible by $2$? Yes, $30 \div 2 = 15$.
• Is $30$ divisible by $3$? Yes, $30 \div 3 = 10$.
• Is $30$ divisible by $6$? Yes, $30 \div 6 = 5$.

This confirms the property: since $30$ is divisible by $6$, it is divisible by all the factors of $6$.

---

Property 2: Divisibility by Co-prime Numbers

If a number is divisible by two numbers that are co-prime (their only common factor is $1$), then the number is also divisible by the product of these two co-prime numbers.

Let's consider the number $72$. $72$ is divisible by $3$ ($72 \div 3 = 24$) and $72$ is also divisible by $4$ ($72 \div 4 = 18$).

First, let's check if $3$ and $4$ are co-prime:

• Factors of $3$ are $1, 3$.
• Factors of $4$ are $1, 2, 4$.

The only common factor of $3$ and $4$ is $1$. So, $3$ and $4$ are co-prime numbers.

According to the property, since $72$ is divisible by $3$ and $4$, and $3$ and $4$ are co-prime, $72$ should be divisible by their product, which is $3 \times 4 = 12$.

Let's check: $72 \div 12 = 6$. Yes, $72$ is divisible by $12$.

Important: This property works only if the two divisors are co-prime. Let's see an example where the divisors are NOT co-prime. Consider the number $36$. $36$ is divisible by $4$ ($36 \div 4 = 9$) and $36$ is divisible by $6$ ($36 \div 6 = 6$). Are $4$ and $6$ co-prime?

• Factors of $4$: $1, 2, 4$.
• Factors of $6$: $1, 2, 3, 6$.

The common factors of $4$ and $6$ are $1$ and $2$. Since the common factors include $2$ (besides $1$), $4$ and $6$ are not co-prime.

Their product is $4 \times 6 = 24$. Is $36$ divisible by $24$? $36 \div 24 = 1$ with a remainder of $12$. No, $36$ is not divisible by $24$. This example shows why the condition of co-prime divisors is necessary for this property to hold.

---

Property 3: Divisibility of Sum

If two numbers are divisible by a certain number, then their sum is also divisible by that same number.

Example: The number $10$ is divisible by $5$ ($10 \div 5 = 2$). The number $15$ is also divisible by $5$ ($15 \div 5 = 3$).

Their sum is $10 + 15 = 25$. Is $25$ divisible by $5$? $25 \div 5 = 5$. Yes, the sum ($25$) is divisible by $5$.

Let's understand why this works. If a number 'a' is divisible by 'k', it means $a$ can be written as 'k' multiplied by some whole number (say 'm'), i.e., $a = k \times m$. Similarly, if another number 'b' is divisible by 'k', it means $b = k \times n$ for some whole number 'n'.

The sum of these two numbers is $a + b$. Substituting the expressions for 'a' and 'b':

$a + b = (k \times m) + (k \times n)$

Using the distributive property of multiplication, we can factor out 'k':

$a + b = k \times (m + n)$

Since $m$ and $n$ are whole numbers, their sum $(m+n)$ is also a whole number. This means that the sum $a+b$ can be expressed as 'k' multiplied by a whole number. Therefore, $a+b$ is divisible by 'k'.

---

Property 4: Divisibility of Difference

If two numbers are divisible by a certain number, then their difference is also divisible by that same number (assuming we subtract the smaller number from the larger one so that the difference is a whole number).

Example: The number $25$ is divisible by $5$ ($25 \div 5 = 5$). The number $10$ is also divisible by $5$ ($10 \div 5 = 2$).

Their difference is $25 - 10 = 15$. Is $15$ divisible by $5$? $15 \div 5 = 3$. Yes, the difference ($15$) is divisible by $5$.

Let's understand why this works. If a number 'a' is divisible by 'k', it means $a = k \times m$ for some whole number 'm'. If another number 'b' is divisible by 'k', it means $b = k \times n$ for some whole number 'n'. Assume $a \ge b$, so $m \ge n$.

The difference of these two numbers is $a - b$. Substituting the expressions for 'a' and 'b':

$a - b = (k \times m) - (k \times n)$

Using the distributive property, we can factor out 'k':

$a - b = k \times (m - n)$

Since $m$ and $n$ are whole numbers and $m \ge n$, their difference $(m-n)$ is also a whole number. This means that the difference $a-b$ can be expressed as 'k' multiplied by a whole number. Therefore, $a-b$ is divisible by 'k'.

Note: This property also applies if one number is divisible by 'k' and the other is not. Their sum and difference will also not be divisible by 'k'. If neither number is divisible by 'k', their sum or difference may or may not be divisible by 'k'.

---

Property 5: Divisibility of Multiples

If a number is divisible by another number, then any multiple of the first number is also divisible by the second number.

Example: The number $10$ is divisible by $5$ ($10 \div 5 = 2$). Let's take a multiple of $10$, say $10 \times 3 = 30$. Is $30$ divisible by $5$? $30 \div 5 = 6$. Yes, the multiple of $10$ ($30$) is divisible by $5$. Let's take another multiple, $10 \times 7 = 70$. Is $70$ divisible by $5$? $70 \div 5 = 14$. Yes, it is.

Let's understand why this works. If a number 'a' is divisible by 'k', it means $a$ can be written as $a = k \times m$ for some whole number 'm'.

Now, consider any multiple of 'a'. A multiple of 'a' is formed by multiplying 'a' by any natural number (say 'n'). The multiple is $a \times n$.

Substitute the expression for 'a' ($a = k \times m$):

$a \times n = (k \times m) \times n$

Using the associative property of multiplication, we can group the numbers differently:

$a \times n = k \times (m \times n)$

Since $m$ and $n$ are whole numbers (or natural numbers), their product $(m \times n)$ is also a whole number. This means that the multiple $a \times n$ can be expressed as 'k' multiplied by a whole number.

Therefore, any multiple of 'a' is divisible by 'k'.

Prime Factorisation

In this chapter, we have explored factors and prime numbers. Now, we will combine these ideas to break down composite numbers into their prime building blocks. Expressing a number as a product of only prime numbers is called prime factorisation.

Every composite number can be written as a multiplication of prime numbers. For example, $6$ is a composite number, and it can be written as $2 \times 3$. Here, $2$ and $3$ are both prime numbers. This is the prime factorisation of $6$.

A very important idea in mathematics is that the prime factorisation of any composite number is unique, meaning there is only one set of prime numbers that will multiply together to make that number (if we ignore the order). For example, $12$ can be written as $2 \times 6$ or $3 \times 4$. But its prime factorisation is always $2 \times 2 \times 3$.

---

Methods of Prime Factorisation

There are two common methods that we use to find the prime factorisation of a number:

1. Factor Tree Method:

In this method, we start by breaking down the given number into any two factors. If a factor is prime, we circle it or stop that branch. If a factor is composite, we further break it down into its factors. We continue this process until all the 'branches' end in prime numbers. The prime numbers at the end of all branches are the prime factors of the original number.

Example: Find the prime factorisation of $36$ using the Factor Tree Method.

We start with $36$ and find two factors. Let's say $4$ and $9$. Neither $4$ nor $9$ are prime, so we break them down further.

• $4$ can be broken down into $2 \times 2$. Both $2$ are prime.
• $9$ can be broken down into $3 \times 3$. Both $3$ are prime.

[Imagine a tree structure: $36$ at the top, branching down to $4$ and $9$. From $4$, branches go to $2$ and $2$. From $9$, branches go to $3$ and $3$. The prime numbers at the ends of the branches are $2, 2, 3, 3$.]

The prime factors found at the ends of the branches are $2, 2, 3,$ and $3$.

So, the prime factorisation of $36$ is $2 \times 2 \times 3 \times 3$.

What if we started with different factors for $36$? Let's say $2$ and $18$.

• $2$ is prime.
• $18$ is composite. Break $18$ into factors, say $2$ and $9$.
• $2$ is prime.
• $9$ is composite. Break $9$ into factors, $3$ and $3$. Both $3$ are prime.

[Imagine a tree structure: $36$ at the top, branching down to $2$ and $18$. From $18$, branches go to $2$ and $9$. From $9$, branches go to $3$ and $3$. The prime numbers at the ends are $2, 2, 3, 3$.]

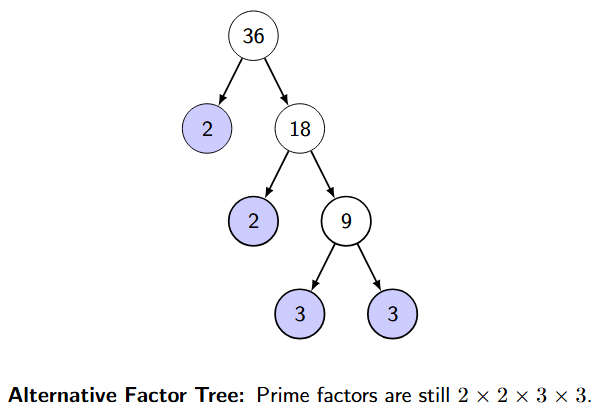
The prime factors are still $2, 2, 3,$ and $3$. This illustrates the uniqueness of prime factorisation.

2. Division Method:

In this method, we repeatedly divide the given number by the smallest possible prime number until the quotient becomes $1$. The prime numbers used as divisors are the prime factors of the number.

We arrange the division steps as shown below:

Example: Find the prime factorisation of $144$ using the Division Method.

Start by dividing $144$ by the smallest prime number, $2$, as $144$ is even.

Keep dividing by $2$ as long as the quotient is even.

When the quotient is no longer divisible by $2$, try the next smallest prime number, $3$.

Continue with the next prime numbers ($5, 7, 11,$ etc.) if needed, until the quotient is $1$.

$$\begin{array}{c|cc} 2 & 144 \\ \hline 2 & 72 \\ \hline 2 & 36 \\ \hline 2 & 18 \\ \hline 3 & 9 \\ \hline 3 & 3 \\ \hline & 1 \end{array}$$

The prime factors are the divisors on the left side of the vertical line. Reading them from top to bottom, they are $2, 2, 2, 2, 3,$ and $3$.

So, the prime factorisation of $144$ is $2 \times 2 \times 2 \times 2 \times 3 \times 3$. This can also be written using exponents as $2^4 \times 3^2$.

---

The Unique Prime Factorisation Property

As we saw with the number $36$, no matter how you factor a composite number using different starting pairs of factors, the final collection of prime factors is always the same. This is a very important property called the Unique Prime Factorisation Theorem (also known as the Fundamental Theorem of Arithmetic). It states that every composite number greater than $1$ can be expressed as a product of prime numbers in one and only one way, except for the order in which the prime factors are written.

For example, the prime factorisation of $12$ is $2 \times 2 \times 3$. Whether you write it as $2 \times 2 \times 3$, or $2 \times 3 \times 2$, or $3 \times 2 \times 2$, the set of prime factors is $\{2, 2, 3\}$. This unique set of prime factors is like the number's fingerprint!

Highest Common Factor (HCF)

In the previous sections, we discussed factors of numbers. Now, we'll learn about finding factors that are common to two or more numbers, and specifically, the largest among them. The Highest Common Factor (HCF) of two or more given natural numbers is the largest number which is a factor of all the given numbers. It is also sometimes known as the Greatest Common Divisor (GCD).

---

Finding HCF by Listing Factors

This is a basic method, especially useful for smaller numbers. It involves listing all the factors of each of the given numbers and then identifying the common factors. The largest number among these common factors is the HCF.

Steps:

1. List all the factors of each of the given numbers.
2. Identify the factors that are common to all the lists (these are the common factors).
3. The largest number among the common factors is the HCF.

Example: Find the HCF of $12$ and $18$ using the Listing Factors method.

• Factors of $12$: $1, 2, 3, 4, 6, 12$
• Factors of $18$: $1, 2, 3, 6, 9, 18$

The common factors of $12$ and $18$ are the numbers that appear in both lists: $1, 2, 3, 6$.

The highest (greatest) among these common factors is $6$.

So, HCF$(12, 18) = 6$.

---

Finding HCF by Prime Factorisation Method

This method uses the prime factorisation of the given numbers. It is generally more efficient for larger numbers compared to listing all factors.

Steps:

1. Find the prime factorisation of each of the given numbers.
2. Identify all the prime factors that are common to all the factorisations.
3. For each common prime factor, take the smallest power (exponent) it appears with in any of the factorisations.
4. Multiply these common prime factors, each raised to its smallest power. The result is the HCF.

Example: Find the HCF of $12$ and $18$ using the Prime Factorisation method.

Step 1: Find the prime factorisation of each number.

So, the factorisations in exponential form are:

• $12 = 2 \times 2 \times 3 = 2^2 \times 3^1$
• $18 = 2 \times 3 \times 3 = 2^1 \times 3^2$

Step 2: Identify the common prime factors.

The prime factors of 12 are {2, 3}.

The prime factors of 18 are {2, 3}.

The common prime factors are 2 and 3.

Step 3: Take the smallest power for each common factor.

• For the prime factor 2: The powers are $2^2$ and $2^1$. The smallest power is 1. So we take $2^1$.
• For the prime factor 3: The powers are $3^1$ and $3^2$. The smallest power is 1. So we take $3^1$.

Step 4: Multiply these to find the HCF.

HCF$(12, 18) = 2^1 \times 3^1 = 2 \times 3 = 6$.

The HCF of $12$ and $18$ is 6.

---

Finding HCF by Long Division Method (Euclidean Algorithm)

This method is particularly useful and efficient for finding the HCF of two large numbers. It is based on the principle that the HCF of two numbers does not change if the smaller number is subtracted from the larger number (or if the larger number is replaced by its remainder when divided by the smaller number). This is known as the Euclidean Algorithm.

Steps:

1. Divide the larger number by the smaller number.
2. Take the remainder as the new divisor and the previous divisor as the new dividend.
3. Repeat the division process.
4. Continue this process until the remainder becomes $0$.
5. The last non-zero remainder is the HCF of the two numbers.
6. If there are more than two numbers, find the HCF of any two numbers first. Then find the HCF of the result and the third number, and so on.

Example: Find the HCF of $135$ and $225$ using the Long Division method.

Divide the larger number ($225$) by the smaller number ($135$):

$$\begin{array}{r} 1\phantom{225)} \\ 135{\overline{\smash{\big)}\,225\phantom{)}}} \\ \underline{-~\phantom{(}135\phantom{)}} \\ 90\phantom{)} \end{array}$$

The remainder is $90$. Now, the new divisor is the previous remainder ($90$) and the new dividend is the previous divisor ($135$). Divide $135$ by $90$:

$$\begin{array}{r} 1\phantom{135)} \\ 90{\overline{\smash{\big)}\,135\phantom{)}}} \\ \underline{-~\phantom{(}90\phantom{)}} \\ 45\phantom{)} \end{array}$$

The remainder is $45$. Now, the new divisor is $45$ and the new dividend is $90$. Divide $90$ by $45$:

$$\begin{array}{r} 2\phantom{90)} \\ 45{\overline{\smash{\big)}\,90\phantom{)}}} \\ \underline{-~\phantom{(}90\phantom{)}} \\ 0\phantom{)} \end{array}$$

The remainder is now $0$. The process stops here.

The last non-zero remainder was $45$.

So, HCF$(135, 225) = 45$.

---

Answer:

Least Common Multiples (LCM)

In the previous section, we learned about the Highest Common Factor (HCF), which is the largest number that divides two or more numbers exactly. Now, we will learn about multiples and finding the smallest multiple that is common to two or more numbers. The Least Common Multiple (LCM) of two or more given natural numbers is the smallest non-zero number that is a multiple of all the given numbers.

Think of it as the smallest number that appears in the multiplication tables of all the given numbers (except for 0, which is a common multiple but not the "least" non-zero one). The term "least" refers to the smallest value, "common" means belonging to all, and "multiple" means a number obtained by multiplying.

---

Finding LCM by Listing Multiples

This is a straightforward method for finding the LCM of smaller numbers. It involves writing down the multiples of each number until you find the first multiple (other than zero) that appears in all the lists of multiples.

Steps:

1. List the multiples of each of the given numbers.
2. Continue listing multiples for each number until you find a number that appears in the lists of all the given numbers.
3. The first (smallest) non-zero number that appears in all the lists is the LCM.

Example: Find the LCM of $12$ and $18$ by Listing Multiples.

• Multiples of $12$: $12 \times 1=12, 12 \times 2=24, \ $$ 12 \times 3=36, \ $$ 12 \times 4=48, \ $$ 12 \times 5=60, \ $$ 12 \times 6=72, \ $$ 12 \times 7=84, ...$
• Multiples of $18$: $18 \times 1=18, 18 \times 2=36, \ $$ 18 \times 3=54, \ $$ 18 \times 4=72, \ $$ 18 \times 5=90, ...$

Now, let's look for numbers that are in both lists. The common multiples of $12$ and $18$ are $36, 72,$ and so on.

The smallest among these common multiples (excluding 0) is $36$.

So, LCM$(12, 18) = 36$.

---

Finding LCM by Prime Factorisation Method

This method uses the prime factorisation of the given numbers, similar to finding HCF, but with a different rule for combining the prime factors.

Steps:

1. Find the prime factorisation of each of the given numbers. Write the factorisation using powers (exponents).
2. Identify all the prime factors that appear in the factorisation of any of the given numbers (both common and non-common prime factors).
3. For each identified prime factor, take the highest power (exponent) it appears with in any of the factorisations.
4. Multiply these prime factors, each raised to its highest power. The result is the LCM.

Example: Find the LCM of $12$ and $18$ using the Prime Factorisation method.

Step 1: Find the prime factorisation of each number.

So, the factorisations in exponential form are:

• $12 = 2 \times 2 \times 3 = 2^2 \times 3^1$
• $18 = 2 \times 3 \times 3 = 2^1 \times 3^2$

Step 2: Identify all unique prime factors involved.

The prime factors that appear in either factorisation are 2 and 3.

Step 3: Take the highest power for each unique factor.

• For the prime factor 2: The powers are $2^2$ and $2^1$. The highest power is 2. So we take $2^2$.
• For the prime factor 3: The powers are $3^1$ and $3^2$. The highest power is 2. So we take $3^2$.

Step 4: Multiply these to find the LCM.

LCM$(12, 18) = 2^2 \times 3^2 = 4 \times 9 = 36$.

The LCM of $12$ and $18$ is 36.

---

Finding LCM by Common Division Method

This method involves dividing the given numbers together by common prime factors. It's often the quickest method for multiple numbers.

Steps:

1. Write the given numbers in a row, separated by commas.
2. Divide the numbers by the smallest prime number that divides at least one of the numbers. Write the prime divisor to the left.
3. Write the quotients and the undivided numbers in the next row.
4. Repeat the division process with the next smallest prime number. Continue until all the numbers in the last row are $1$.
5. The LCM is the product of all the prime divisors used and the numbers in the last row (which will all be $1$). Or, if you stop when no two numbers have a common prime factor, the LCM is the product of the divisors and the remaining numbers in the last row. The method below continues until the last row is all $1$s.

Example: Find the LCM of $12$ and $18$ using the Common Division method.

$$\begin{array}{c|cc} 2 & 12 \;, & 18 \\ \hline 3 & 6 \; , & 9 \\ \hline 2 & 2 \; , & 3 \\ \hline 3 & 1 \; , & 3 \\ \hline & 1 \; , & 1 \end{array}$$

Explanation of steps:

• Divide $12$ and $18$ by $2$ (smallest prime, divides both). Quotients are $6$ and $9$.
• Divide $6$ and $9$ by $3$ (next smallest prime that divides at least one). Quotients are $2$ and $3$.
• Divide $2$ and $3$ by $2$ (smallest prime that divides at least one, which is $2$). Quotient of $2$ is $1$. $3$ is not divisible by $2$, so we bring it down.
• Divide $1$ and $3$ by $3$. $1$ is brought down. Quotient of $3$ is $1$.
• Stop when all numbers in the last row are $1$.

The LCM is the product of all the divisors on the left:

LCM$(12, 18) = 2 \times 3 \times 2 \times 3 = 36$.

So, LCM$(12, 18) = 36$.

---

Answer:

Relation between HCF and LCM of Two Natural Numbers

For any two natural numbers, there exists an important and useful relationship between their Highest Common Factor (HCF) and their Least Common Multiple (LCM).

---

Property: Product of Two Numbers = Product of their HCF and LCM

This property states that for any two given natural numbers, the product obtained by multiplying the two numbers is always equal to the product obtained by multiplying their HCF and LCM.

Let the two natural numbers be 'a' and 'b'. Their HCF is HCF(a, b) and their LCM is LCM(a, b).

The relationship is given by the formula:

Product of two numbers $=$ HCF $\times$ LCM

This can be written using symbols as:

$a \times b =$ HCF$(a, b) \times$ LCM$(a, b)$

---

Verification with an Example

Let's verify this property using the numbers $12$ and $18$. From our previous calculations:

• The HCF of $12$ and $18$ is $6$.
• The LCM of $12$ and $18$ is $36$.

Now, let's find the product of the two numbers:

Product of numbers $= 12 \times 18 = 216$.

Next, let's find the product of their HCF and LCM:

Product of HCF and LCM $= 6 \times 36$.

Let's perform the multiplication:

$$\begin{array}{cc} & & 3 & 6 \\ \times & & & 6 \\ \hline & 2 & 1 & 6 \\ \hline \end{array}$$

Product of HCF and LCM $= 216$.

Since the product of the numbers ($216$) is equal to the product of their HCF and LCM ($216$), the property is verified for the numbers $12$ and $18$. This property holds true for any pair of natural numbers.

---

Using the Relation to Find HCF or LCM

The relationship $a \times b =$ HCF$(a, b) \times$ LCM$(a, b)$ can be rearranged using division to find the HCF or LCM of two numbers if the other values are known:

• If you know the numbers 'a' and 'b' and their LCM, you can find the HCF:
  HCF$(a, b) = \frac{a \times b}{\text{LCM}(a, b)}$
• If you know the numbers 'a' and 'b' and their HCF, you can find the LCM:
  LCM$(a, b) = \frac{a \times b}{\text{HCF}(a, b)}$

Important Note: This valuable relationship between the product of numbers and the product of their HCF and LCM is applicable only for two numbers. It does not work for finding the HCF and LCM of three or more numbers.

---

Answer: